Boolean Expressions-2

Author : Sachidananda Reddy, Digital Design Engineer, SignOff Semiconductors

Author : Poojitha Palem, Digital Design Engineer, SignOff Semiconductors

We hope you had a good understanding of Boolean Expressions which is available @ Boolean Expressions. In this blog, we will discuss on the simplification of boolean functions.

KARNAUGH MAP:

The Karnaugh map also known as Veitch diagram or simply as K map. It provides simple straight forward procedure for minimizing Boolean functions

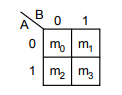
Figure 1: 2-variable Boolean function

Figure 2: 3-variable Boolean function

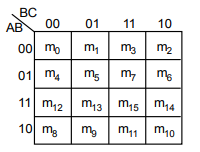
Figure 3: 4-variable Boolean function

In K-Map, gray code is used to arrange the bits. Because, the boolean simplification is done by grouping adjacent cells that have 1. To get the simplified expression, the adjacent cells must have 1 bit change.

MINIMIZATION OF SOP EXPRESSIONS:

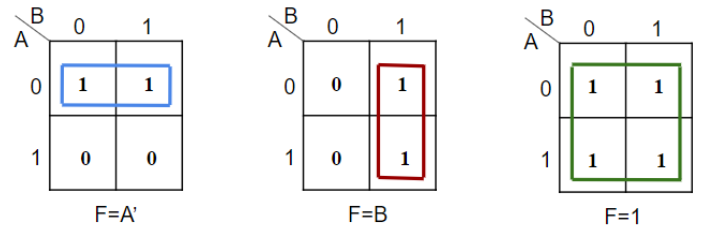
Figure 4

MINIMIZATION OF POS EXPRESSIONS:

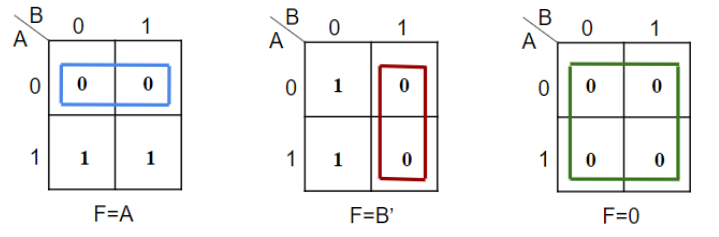
Figure 5

MINIMIZATION OF POS EXPRESSIONS:

• Plot all ones in the function truth table on the map.
• Combine adjacent 1’s into a group of one, two, four, eight, sixteen. The group of minterm should be as large as possible.
• In a four variable karnaugh map,

1. 1. variable product term is obtained if 8 adjacent squares are covered.
   2. variable product term is obtained if 4 adjacent squares are covered.
   3. variable product term is obtained if 2 adjacent squares are covered.

• The final stage is reached when each of the group of minterms are ORed together to form the simplified sum of product expression.

For example,

To simplify F(A,B,C,D) = ∑( 0,1,2,10,11,14 ) + d( 5,8,9 ) in SOP form. Here, d represents don’t cares.

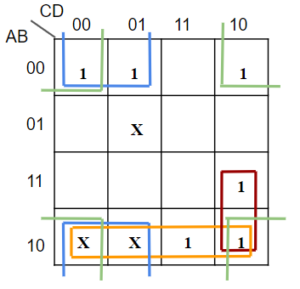
Figure 6

1’s and d’s (Xs) are combined in order to enclose the maximum number of adjacent squares with 1. As shown in K-map in above figure, by combining 1’s and d’s (Xs), three quads can be obtained. The X in square 5 is left free since it does not contribute in increasing the size of any group. Therefore,

I Quad covers minterms 0, 2, 10 and d8 ——-> B’D’

II Quad covers minterms 10, 11 and d8, d9 ——–> AB’

III Quad covers minterms 0, 1 and d8, d9 ———> B’C’

A pair covers minterms 10 and 14 ———> ACD’

So, F = B’D’ + AB’ + B’C’ + ACD’

To simplify F(A,B,C,D) = ∑(0,2,3,5,7,10,11,15) in POS form,

We need to map for 0s and then take the compliment of that function to get F in POS form

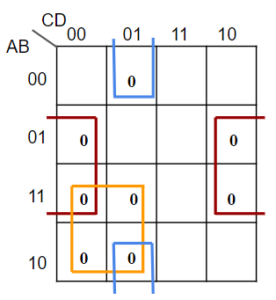
Figure 7

F= (AC’ + BD’ + B’C’D)’ = (A’+C) (B’+D) (B+C+D’)

IMPLICANT :

In Boolean logic, an implicant is a “covering” (sum term or product term) of one or more minterms in a sum of products (or maxterms in a product of sums) of a boolean function.

Prime Implicant:

Each square made up of the bunch of adjacent minterms is called a subcube. Each of these subcubes is called a prime implicant.

Ex: For example, F(A,B,C,D) = ∑( 0,2,3,4,9,10,12,13 ) + d( 6,8,14 )

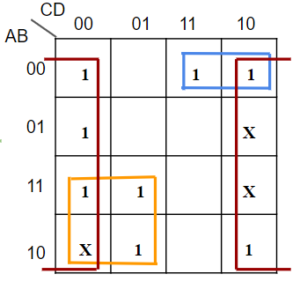
Figure 8

Prime Implicants are D’, AC’, A’B’C

The simplified expression is Y= D’ + AC’ + A’B’C

Essential Prime Implicant:

The prime implicant which contains atleast one 1 which cannot be covered by any other prime implicant is called an essential prime implicant.

Figure 9

Redundant Prime Implicant:

The prime implicant whose each 1 is covered by atleast one essential prime implicant is called a redundant prime implicant.

Figure 10

False Prime Implicant:

The maxterms are called false minterms. The prime implicants obtained by using the maxterms are called false prime implicants.

Essential False Prime Implicant:

The false prime implicants which contains atleast one 0 which cannot be covered by any other false prime implicant is called an essential false prime implicant.

Redundant False Prime implicant:

The false prime implicant whose each 0 is covered by atleast one essential false prime implicant is called a redundant false prime implicant.

Selective False Prime Implicant:

A false prime implicant which is neither an essential false prime implicant nor a redundant false prime implicant is called a selective false prime implicant.

FIVE VARIABLE K-MAP:

The Karnaugh map becomes three dimensional when solving logic problems with more than four variables. A three dimensional K-map will be used here. The 5 variable M-map contains 25 = 32 squares. Instead of representing a single 32-square map, two 16-square K-maps are generally used.

Figure 12

In order to identify the adjacent grouping in the 5-variable maps, we must imagine that the two maps are superimposed on one another as shown in the figure.

Figure 13

Every square in one map is adjacent to the corresponding square in the other map, because only one variable, changes between such corresponding squares.

Figure 14

SIX VARIABLE K-MAP:

A six variable K-map contains 26 = 64 squares. These squares are divided into four identical 16-square maps as shown in the figure.

Figure 15

In order to identify the adjacent groupings in the 6-variable maps, we must imagine that the 4 maps are superimposed on one another.

Figure 16

Methods to find number of minterms for F(A,B,C,D) = A + B’

Method-1:

Figure 17

F(A,B,C,D) = ∑m (0,1,2,3,8,9,10,11,12,13,14,15)

Therefore, Number of minterms = 12

Method-2:

In m-variable K-Map, grouping of 2n number of cubes results (m-n) variables by eliminating n variables.

n(A) we have m=4, n=3 ——-> n(A) = 2n = 23 = 8

n(B’) we have m=4, n=3 ——-> n(B’) = 2n = 23 = 8

n(AB’) we have m=4, n=2 ——–> n(AB’) = 2n = 22 = 4

n(A U B’) = n(A) + n(B’) – n(AB’)

= 8 + 8 – 4 = 12

If A and A’ are present in the same expression like AB+A’ then n(AA’B) = 0

Method-3:

This method is similar as a normal K-map method. Draw K-map for A+B’ then we will get the number of minterms as 12.

Questions to try:

1. Implement AND-OR logic of a circuit, using minimum gates, that gives the output as HIGH when the input is BCD equivalent of 4,6 or 8 and LOW otherwise.
2. What is the number of Essential Prime Implicants and Redundant Prime Implicants for the following function                                    F (A,B,C,D) = Σm(0,2,7,9,11) + d(3,8,10,14)
3. Simplify the Boolean function F(A, B, C, D, E) = Σ(0, 1, 4, 5, 16, 17, 21, 25, 29, 30).
4. Simplify the Boolean function F(A, B, C, D, E, F) = Π(6, 9, 13, 18, 19, 27, 29, 41, 45, 57, 61, 63).
5. Using a Karnaugh map simplify the following equations

• • • X = D̅(A̅[C̅+B̅C] + A(C̅+B̅C]) +BCD̅
    • X = A̅B̅C̅ + B̅CD̅ + A̅BD + ABCD +AC̅D + A̅BC̅D
    • X = D̅E̅ + B̅CDE + C̅E̅ + ABC̅