Boolean Expressions-1
Author : Sachidananda Reddy, Digital Design Engineer, SignOff Semiconductors
Author : Poojitha Palem, Digital Design Engineer, SignOff Semiconductors
We hope you had a good understanding of Logic Gates which is available @ Logic Gates. To reduce the logical complexities of any Boolean expression, a set of theorems have been developed which is explained below.
BOOLEAN THEOREMS:
Boolean algebra helps to analyze a logic circuit and express its operation mathematically. We have several Boolean Theorems that helps us to simplify logic expressions and logic circuits.
Single Variable Theorems:
| AND Operation | OR Operation |
|---|---|
| A . 0 = 0 | A + 0 = A |
| A . 1 = A | A + 1 = 1 |
| A . A = A | A + A = A |
| A . A’ = 0 | A + A’ = 1 |
Multivariable Theorems:
The multivariable theorems involves more than one variable.
Commutative laws:
- A + B = B + A
- A . B = B . A
Associative laws:
- A + (B + C) = (A + B) + C = A + B + C
- A (BC) = (AB) C = ABC
Distributive laws:
- A (B + C) = AB + AC
- A + BC = (A+B) (A+C)
- (A + B) (C + D) = AC + AD + BC + BD
Absorption laws:
- A + AB = A
- A (A + B) = A
Redundant Literal Rule:
- A + A’B = A + B
- A’ + AB = A’ + B
- A(A’ + B) = AB
Demorgan’s Theorem:
- (A+B)’ = A’ . B’
- (AB)’ = A’ + B’
This law can be extended to any number of variables or combinations of variables.
How to apply Demorgan’s theorem to an expression?
- Complement the entire given expression.
- Change all the AND’s to OR’s and all the OR’s to AND’s.
- Complement each of the individual variables.
- Change all 0s to 1s and all 1s to 0s.
This procedure is called as Demorganization or Complementation of switching expressions. In simple words, we can say it as ‘Break the line, change the sign’.
f(A, B, ………, 0, 1, . , +) = f(A’, B’, ………., 1, 0, +, .)
Consensus Theorem:
- AB + A’C + BC = AB + A’C
- (A + B)(A’ + C)(B + C) = (A + B)(A’ + C)
If one term is containing A and the other term is containing A’ and the third term containing the left-out literals of the first two terms then the third term is redundant. It means the function remains same with and without the third term.
This theorem can be extended to any number of variables.
AB + A’C + BCD = AB + A’C
(A + B)(A’ + C)(B + C + D) = (A + B)(A’ + C)
Transposition Theorem:
AB + A’C = (A + C)(A’ + B)
DUAL OF A BOOLEAN FUNCTION:
The DUAL of a boolean function is obtained by interchanging OR and AND operations and replacing 1’s by 0’s and 0’s by 1’s.

For example, DUAL of (ABCD…F)’ = A’ + B’ + C’ + D’ + … + F’
COMPLEMENT OF A BOOLEAN FUNCTION:
To compute the complement of a boolean function, we use Demorgan’s theorems.
How to complement a boolean function?
- Parenthesize product terms.
- Take the dual of a function.
- Complement each literal.
For example, F(A,B,C) = AB’ + BC’ + A’C’
F'(A,B,C) = (AB’ + BC’ + A’C’)’
= (AB’)’ . (BC’)’ . (A’C’)’
= A’B . B’C . AC
REDUCING BOOLEAN EXPRESSIONS:
Realization of a digital circuit with the minimal expression results in reduction of cost and complexity and the corresponding increase in reliability.
How to reduce Boolean Expressions?
- Multiply all variables necessary to remove parentheses.
- Look for identical terms. Only one of those terms be retained and all others are dropped. For example, AB+AB+AB+AB=AB
- Look for a variable and its negation in the same term. This term can be dropped. For example, A + BB’C = A
- Look for pair of terms that are identical except for one variable which may be missing in one of the terms. The larger term can be dropped. For example, ABCD + ABC = ABC
- Look for pair of terms which have the same variables with one or more variables complemented. If a variable in one term of such a pair is complemented while in the second term it is not, then such terms can be combined into a single term with that variable dropped. For example, ABC’D’ + ABC’D = ABC’
SUM OF PRODUCTS FORM (SOP):
The sum of products expressions consists of two or more AND terms (products) that are ORed together. Some examples of this form are:
A’BC+DE’F
AB+C’D+EF+G’H
Note that in sum of products expression, one inversion sign cannot cover more than one variable in a term. For example, we cannot have (AB)’C+(XYZ)’.
PRODUCT OF SUMS FORM (POS):
The product of sums expressions consists of two or more OR terms (sums) that are ANDed together. Some examples of this form are:
(A + B’ + C)(D’ + E’)
(A + B)(D + E’)(X + Y)Z
Minterm and Maxterm for three binary variables:
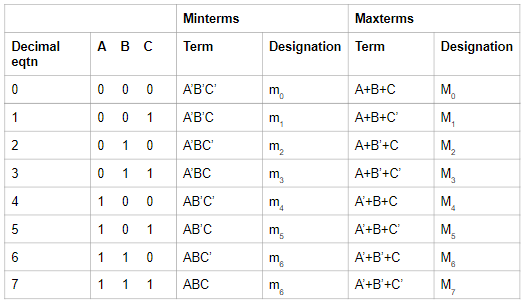
For example,
To convert SOP to POS,
- The SOP function is F = ∑( 1,4,6 )
The POS function is π( 0,2,3,5,7)
- If the SOP function is F(A,B,C) = AB + B’C + A’C’
To get it in POS form, apply Demorgan’s law twice i.e F'(A,B,C) = (AB+B’C+A’C’)’
F'(A,B,C) = (AB)’ . (B’C)’ . (A’C’)’
= (A’+B’) . (B+C’) . (A+C)
= (A’B+A’C’+B’B+B’C’) . (A+C)
= A’BC+AB’C’
F”(A,B,C) = (A’BC + AB’C’)’
= (A’BC)’ . (AB’C’)’
= (A+B’+C’) . (A’+B+C)
CANONICAL FORM:
Any Boolean function that is expressed as a sum of minterms or as a product of max terms is said to be in its canonical form or standard form.
For sum (OR) of min terms(1), The representation of the equation will be
F(list of variables) = ∑(list of min-term indices)
For product (AND) of max terms(0), The representation of the equation will be
F(list of variables) = π(list of max-term indices)
How to convert Canonical forms?
- First, we should interchange the ∑ and π.
- Write the indices of missing variables of the given Boolean function.
For example,
To convert SOP to POS,
- The SOP function is F = ∑( 1,4,6 )
The POS function is π( 0,2,3,5,7)
- If the SOP function is F(A,B,C) = AB + B’C + A’C’
To get it in POS form, apply Demorgan’s law twice i.e F'(A,B,C) = (AB+B’C+A’C’)’
F'(A,B,C) = (AB)’ . (B’C)’ . (A’C’)’
= (A’+B’) . (B+C’) . (A+C)
= (A’B+A’C’+B’B+B’C’) . (A+C)
= A’BC+AB’C’
F”(A,B,C) = (A’BC + AB’C’)’
= (A’BC)’ . (AB’C’)’
= (A+B’+C’) . (A’+B+C)
To convert POS to SOP,
- The POS function is F = π( 1,3,5,7 )
The SOP function is ∑( 0,2,4,6)
- If the POS function is F(A,B,C) = (A+B’+C’) . (A’+B+C)
To get it in SOP form, apply Demorgan’s law twice i.e
F'(A,B,C) = ((A+B’+C’) . (A’+B+C))’
= (A+B’+C’)’ + (A’+B+C)’
= A’BC + AB’C’
F”(A,B,C) = (A’BC + AB’C’)’
= (A’BC)’ . (AB’C’)’
= (A+B’+C’) . (A’+B+C)
= AB+AC+A’B’+B’C+A’C’+BC’
= AB + B’C + A’C’
How to convert SOP to standard SOP form or canonical SOP form?
- Multiply each non-standard product term with the sum of its missing variable and its complement.
- Repeat the above step until all resulting product terms contain all variables.
For example, F = AB + BC + CA
= AB(C+C’) + BC(A+A’) + CA(B+B’)
= ABC+ABC’+BCA+BCA’+CAB+CAB’
= ABC+ABC’+BCA’+CAB’
How to convert POS to standard POS form or canonical POS form?
- Add each non-standard sum term to the product of its missing variable and its complement.
- Apply Boolean law, A+BC = (A+B) (A+C)
- Repeat until all resulting sum terms contain all variables.
For example, F = (A’+B) (B’+C) (A+B+C)
= (A’+B+CC’) (B’+C+AA’) (A+B+C)
= (A’+B+C) (A’+B+C’) (B’+C+A) (B’+C+A’) (A+B+C)
Questions to try:
- Which gates are used for parity generators?
- Boolean algebra is essentially based on ____ [a. numbers b. truth c.logic d. symbols]
- How many possible minterms or maxterms are there for n number of inputs?
- How many unique boolean functions can exist for n number of inputs?
- How many number of duals of distinct Boolean expressions are there for n variables?
- The lift door should open if the lift is stopped, it is level with the floor, and the timer has not expired, or if the lift is stopped, it is level with the floor, and a button is pressed. If O ” Lift door opens ; S ” Lift is stopped ; L ” Level with floor ; X ” Timer expired ; B ” Button pressed Which of the following Boolean expression represents the above condition? [a. O=SLX’+SLB b. O=SLX’B c. O=SL+X’B d.O=(S+L’)X’B]
- Reduce F = (A+BD) (ABC+C’D) using Boolean Theorems (Upto 2 terms).
Comments are closed.
